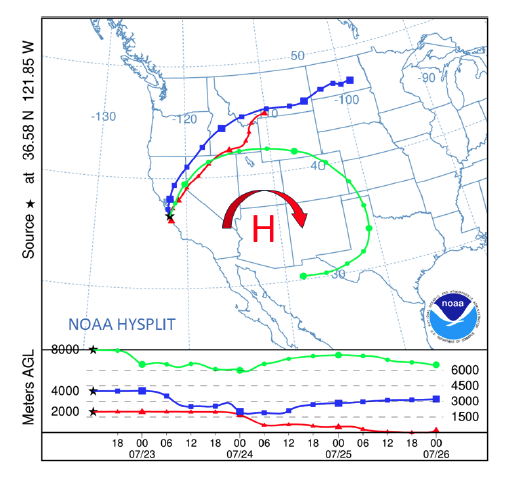
A simulation of three balloon trajectories. (Image courtesy of the instructor. The trajectories were computed by the NOAA HYSPLIT system.)
This essay introduces the two methods that are widely used to observe and analyze fluid flows, either by observing or calculating the trajectories of specific fluid parcels, which yields what is commonly termed a Lagrangian representation, or by observing or calculating the fluid velocity at fixed positions, which yields an Eulerian representation. Lagrangian methods will sometimes be the most efficient and effective way to sample a fluid flow. As well, the physical conservation laws are inherently Lagrangian, since they apply to identifiable fluid volumes rather than to the fluid that happens to be present at a fixed point in space. Nevertheless, the Lagrangian equations of motion applied to a three-dimensional continuum are awkward for many applications, and thus the majority of the theory in fluid mechanics has been developed within the Eulerian system. The premise of this essay is that an improved understanding and appreciation of both systems will help you build the framework for your continued study of fluid mechanics.
Online Textbook
Part 1: Kinematics and the Equations of Motion (PDF)
Part 2: Advection of Parcels and Fields (PDF)